Reflection, what is it and how is it used in psychology?

There are two main ways to define sets: enumeration and description of its elements. Enumeration consists of obtaining a complete list of elements of a set, and description consists of specifying a property that the elements of a given set have, but all others do not.

4. The intersection of two sets is a set consisting of all common elements of these sets.

Example: Let's take the numbers 12 and 18. Let's find their divisors, denoting the entire set of these divisors by the letters A and B, respectively: A = <1, 2, 3, 4, 6, 12>, B = <1, 2, 3, 6, 9, 18>.

We see that the numbers 12 and 18 have common divisors: 1, 2, 3, 6. Let's denote them with the letter C: C = <1, 2, 3, 6>.

The set C is the intersection of the sets A and B. It is written like this: A ∩B =C.

If two sets have no common elements, then the intersection of these sets is the empty set . An empty set is denoted by the sign Ø, and the following notation is used:

X ∩Y = Ø.

The union of two sets is a set consisting of all the elements of these sets.

For example, let's return to the numbers 12 and 18 and the set of their elements A and B. Let's first write down the elements of set A, then add to them those elements of set B that are not in set A. We get the set of elements that A and B have together. Let's denote it by the letter D:

Set D is the union of sets A and B. It is written like this:

D =A U B.

A U B= <1, 2, 3, 4, 6, 12, 9, 18>.

5. The Cartesian product of sets A and B is the resulting set of pairs of the form (x,y), constructed in such a way that the first element is from set A, and the second element of the pair is from set B. Conventional notation:

Products of three or more sets can be constructed as follows:

Examples

1. Let's put A=<1,2>,B=<3,4>. Then the result of the Cartesian product can be written as follows: A×B=<(1,3),(1,4),(2,3),(2,4)>, and B×A=

2.If in the previous example we put B=A, it is obvious that A×B=B×A=

6. Set A

and
B
is the set of elements that belong to
A
and do not belong

to
B. Designate A B
and read “the difference between
A
and
B.
”

Example 1. Let A

there is a segment [1, 3],
B
– a segment [2, 4];
then the union will be the segment [1, 4], the intersection will be the segment [2, 3], the difference A B
will be the half-interval [1, 2],
B A
will be the half-interval (3, 4).

Example 2. Let A

there is a set of rectangles,
B
is the set of all rhombuses in the plane.
Then there is the set of all squares, A B
is the set of rectangles with unequal sides,
B A
is the set of all rhombuses with unequal angles.

7. The intersection of sets is a binary operation on an arbitrary Boolean;

§ The operation of intersection of sets is commutative :

§ The operation of intersection of sets is transitive :

§ The universal set is a neutral element of the operation of intersection of sets:

§ Thus, a Boolean, together with the operation of intersection of sets, is an Abelian group;

§ The operation of intersection of sets is idempotent :

§ If is an empty set , then

8 . The union of sets is a binary operation on an arbitrary Boolean

§ The operation of combining sets is commutative:

§ The operation of combining sets is transitive:

§ The empty set is a neutral element of the set union operation:

§ Thus, the Boolean, together with the operation of union of sets, is a monoid;

§ The operation of intersection of sets is idempotent:

Types of relationships

1.Binary relation (binomial relation). A binary relation in mathematics is a binary relation between any two sets and , that is, any subset of the Cartesian product of these sets: [1]. A binary relation on a set is any subset; such binary relations are most often used in mathematics, in particular, equality, inequality, equivalence, and order relations.

2. A ternary relation is the same as a three-place relation (three-term relation).

3. A quaternary relation is the same as a quaternary relation (four-term relation)

10. A reflexive relation in mathematics is a binary relation on the set in which every element of this set is in a relation with itself.

Formally, a relation is reflexive if .

The property of reflexivity for given relations by a matrix is characterized by the fact that all diagonal elements of the matrix are equal to 1; given relations by the graph, each element x

has a loop - arc (
x
,
x
).

A binary relation on a set is reflexive if and only if its subset is an identical relation on the set ( ), that is.

If this condition is not satisfied for any element of the set, then the relation is called anti-reflexive (or irreflexive ).

If the anti-reflexive relation is given by a matrix, then all diagonal elements are zero. When such a relationship is specified by a graph, each vertex does not have a loop—there are no arcs of the form ( x

,
X
).

What is reflection and reflexivity

“Reflecto” translated from Latin means “return back.” The same term in French sounds like “reflexio” and means “thinking, reflection.”

Initially, the concept of reflection appeared in philosophy as a tool for observing the external world and a way of understanding human existence.
Through the analysis of phenomena occurring in nature and society, a person gets to know himself, seeks ways for survival and self-improvement. Today, the process of reflection is studied and used in other fields, in sociology and psychology. Reflection is a person’s look inside himself, analysis of his thoughts and actions and rethinking them.
But this process is not thoughtless, but based on acquired knowledge and experience, examined through one’s own mistakes. In addition, in sociology it is the ability to evaluate other people and make comparisons between them and oneself.

Reflexivity is the ability to analyze oneself, identify the motives of one’s own actions, including:

past actions and events;
successful or unsuccessful performance results;
emotional state;
personality traits and character that change over time.

The degree of reflection is different for each person and depends on the level of knowledge, intelligence, and upbringing. Some people constantly think about their actions and their motives, while others don’t think about them at all. An important role in this is played by a person’s desire to realize his misconceptions and mistakes, the ability to self-criticize and the need to compare himself with the people around him.

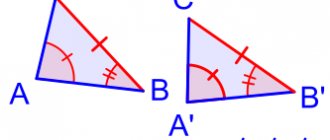
Equivalence relation

A relation R that has the properties of reflexivity, symmetry and transitivity is called an equivalence relation . For equivalent relations, the notation is usually written (read: "equivalent"). Equivalent relations are: “to be congruent” on a set of flat triangles, “to be the same size” on a set of shoe samples, “to be related” on a set of people, etc.

The introduction of an equivalence relation R on a set M determines the partition of all elements of this set into equivalence classes. The set of all equivalence classes forms the factor set of the set M and is denoted M/R. Moreover, each element of this class is an authorized representative of this class. A set of one and only one representative of each class is called a system of representatives of the corresponding equivalence relation. An example of the introduction of an equivalence relationship and the formation of a system of representatives is the formation of a representative body of power based on elections.

Reflection in psychology

A sign of a mature person is the ability to accept responsibility for her actions and the life she has. If a person constantly blames others and circumstances for what happens to him, he is considered weak. Changing your worldview can be difficult.

Reflection in psychology is used precisely for such purposes. As a separate, independent topic in psychology, reflection was highlighted by A. Busemann. This scientist suggested that this process is nothing more than the transfer of circumstances of the external world to oneself.

In Russian science, the problems of reflection were studied by such scientists as L.S. Vygotsky, S.L. Rubinstein, B.V. Zeigarnik. In their opinion, the basis of the concept is thinking, leading to self-understanding, the ability to find the motivation for one’s actions, and answers to questions about personal characteristics. Scientists first defined reflection as an opportunity to “learn the truth about oneself.”

Today, reflection is one of the main directions in psychology used to expand the client’s consciousness. For example, if a person is stressed due to negative daily thoughts, but does not understand this, then he will not be able to get rid of his bad mood. In this case, it is possible to stop suffering only by understanding the underlying cause of the decadent mood, and by determining steps to eliminate it.

With a conscious decision, you can stop the flow of unnecessary thought forms and accept yourself in the “here and now” state. The specialist encourages you to look at yourself “from the outside,” as if at the hero of a series on a TV screen. The goal of a good psychologist is to teach independent introspection and obtain answers to nagging questions. Within psychology, reflection and introspection are identical concepts.

When analyzing a certain situation or action, it is necessary to realize and work through the following points:

A person’s sense of self at the current moment in time. What he experiences: anger, fear, shame, guilt, resentment, etc.
A weak point in self-awareness that has been damaged by events that have occurred. For example, inflated expectations regarding the behavior of a spouse or other family members, which led to resentment.
The ability to use the situation, as well as the difficulties that arise, to your advantage.

Reflection promotes understanding of how a person is perceived from the outside, and not just for self-analysis. The result of reflectivity is self-analysis, the formation of desired personal characteristics, and an understanding of the connection between actions and results.

Psychological reflection functions in the following directions:

Consciousness control, which includes awareness of one’s own thoughts and actions. Formation of logical thinking.
Understanding your strengths and weaknesses is self-criticism. The ability to recognize the relationship between current events, successes, failures and actions taken.
Finding the keys to solving complex problems and tasks. The ability to plan your steps to achieve goals.
Getting rid of destructive, destructive attitudes and thought forms.
Finding opportunities to make thoughtful, correct, useful decisions.
Accumulation and identification of latent abilities, talents and resources.

There is an opinion in psychology that reflection is not always good. In practice, there are cases when soul-searching and excessive thinking led to negative consequences (“woe from mind”, “many knowledge, many sorrows”). For this reason, it is important to learn to reflect competently, preferably accompanied by an experienced specialist.

Order relation

A relation R that has the properties of reflexivity, antisymmetry and transitivity is called an order relation . If an order relation is introduced on a given set, then this set is called ordered. In this case, instead of writing A set is perfectly ordered if for any two elements and from the set M

either , or holds. Otherwise, the set is said to be partially ordered . For example, the relation “to be taller” on the set of trees is perfectly ordered, and the relation “to be a divisor” on the set of integers is partially ordered.

Let each element from the set M, according to some rule f, be assigned a real number, the weight of the element . Entering a weight for each element allows you to order them as their weights increase (decrease) and then compare the elements according to the assigned weight. Examples of ordering through the introduction of weights are: assigning each product its price, each machine its reliability, each body its weight, volume, etc. Weighing decision options through the formation of a complex quality indicator is one of the most common ways to solve the problem of choice based on a variety of different quality attributes.

If a relation has the properties of anti-reflexivity, asymmetry and transitivity, then it is called a relation of strict order (denoted by ). An example of a strict order relation is the order of letters in a fixed alphabet. The ordering of letters in the alphabet allows, in turn, to order words in dictionaries (lexicographic ordering of words).

Concept of self-reflection

Self-reflection is often identified with reflection. This is partly true. The difference between the concepts is that the prefix “self” indicates a reflection of oneself, and not just the external world, events and other people.

Self-reflective people constantly listen to their own feelings and emotions and try to analyze them. Such exercises are very useful for understanding your own self, personal desires and needs. How often do we focus on the expectations of other people, looking for an assessment of our actions from the outside. As a result, one’s own dreams and internal needs remain unfulfilled.

Young people enter training in prestigious professions, and their souls are drawn to creative delights. As a result, the profession does not bring satisfaction, but the parents are happy! A person lives an uninteresting life, suppressing existing talents.

There is another side. In hypertrophied cases, a person constantly listens to emotions. He becomes fixated on personal experiences and becomes neurotic, not seeing the outside world, which is beautiful. A person stops enjoying life, constantly analyzing his own condition.

In this case, it is important to get out of yourself in time, take a deep breath, feel material things: table, floor, wall, hands, feet, sounds and smells.

Many people are wary of their own body signals. Often, excessive reflection leads to neurotic diseases, for example, hypochondria (a pathological condition in which we find ourselves with all possible and impossible diseases).

Cases have been recorded when women find all the signs of pregnancy, and only the results of repeated laboratory examinations (for example, ultrasound) can dissuade them from this. Of course, if you suspect a disease, you must undergo a medical examination. But when a person realizes that his fears are far-fetched, he should move away from focusing on personal feelings and ignore them.

Forms and types of reflection

We described reflection as a complex process directed both within oneself and into the external world, leading to benefit for the individual, or, on the contrary, to its destruction. Let's consider what forms and types of introspection exist in psychology.

From the point of view of the impact on the future state of a person:

Correct constructive self-analysis, which allows you to understand yourself, draw logical conclusions and not step on familiar mistakes again.
Harmful destructive self-analysis, leading to neurotic disorders and deep fixation on problems, often imaginary. In such situations, feelings of guilt, helplessness and hopelessness are cultivated. A person needs the help of a specialist.

Taking into account time periods, reflection occurs:

Event-based or situational . The individual analyzes a problem that takes place in the present time, “here and now.”
Retrospection , looking to the past. A person evaluates past events and his actions, draws conclusions about their correctness and timeliness.
Perspective , facing future events. The individual plans further actions and events based on self-analysis.

Based on the object of study, the process can be divided into the following forms:

Self-reflection , turning to one’s own inner world, personal experiences and emotions.
Communicative . In this form, reflection is devoted to other people, interaction with friends, relatives, and colleagues. A person tries to analyze relationships and interactions.
Sanogenic is a type of self-analysis in which a substantive study of strong emotions is carried out, a search for means to minimize or eliminate unnecessary suffering and experiences.
Intelligent . The individual’s attention is focused on the application of knowledge, skills, and the possibilities of their use in the material world.

A combination of forms of reflection under given conditions gives the best results; it is always necessary to combine methods of analysis for a specific situation.

What does it mean to reflect?

To reflect is to think, to think logically, to analyze actions and actions, to know oneself.

Is it worth understanding your personality? Of course yes. If a person has not understood himself, he is led by others and lives someone else’s life. Low self-esteem, complexes, and feelings of guilt sit deep inside and interfere with further development. They need to be found and neutralized.

By reflecting, we learn:

Think rationally.
Stop mental “garbage”.

A low level of self-analysis is the path to making the same mistakes and blunders throughout your life. At the everyday level, the concept of a reflective person is often associated with such definitions as: “to be nervous”, “to worry”, “to worry too much”. Therefore, in any action, moderation and reasonableness are important.

It is necessary to approach your inner world soberly and calmly, without allowing emotions to overwhelm the arguments of reason. A person who knows how to reflect is his own psychoanalyst; not everyone is capable of this.

In order to “self-examine” for the benefit of your business, you need to avoid the following mistakes:

You should think about the motives for your actions, not the actions themselves . For example, a husband who cheated on his wife may realize his betrayal and vow not to do it again. But if a man does not understand what pushed him to cheat, no force will stop him from repeating the mistake, since the motives for the need to go “to the left” will remain undeveloped.
“Saw sawdust ,” as D. Carnegie said. This means constantly grinding past sins and failures in your head, coming up with possible other consequences of what has already happened. What was is no longer there, think about the current moment, make plans for the future.
Cultivate feelings of guilt . Yes, we made a mistake, but we got our lesson for it. There is no point in berating yourself for something that cannot be fixed. Everything is not without sin.
Responsible for the whole world . Processes in the world occur against our will. We should not take responsibility for something we cannot influence.

If you follow the rules outlined, then reflection is not only possible, but also useful.

Properties of relationships

Reflexivity . A relation R defined on a set M is called reflexive if for any relation it holds. Formally, reflexivity can be defined as follows: A reflexive relation always holds between the object and itself. The most striking examples of reflexive relationships are self-care and equality.

Anti-reflexivity. A relation R defined on a set M is anti-reflexive if In anti-reflexive relations it follows from the condition that Examples of anti-reflexive relations: to be older, to be smaller, etc.

Symmetry. A relation R defined on a set M is called symmetric if, when the relation is satisfied, the relation is also satisfied. Formally, the relation is symmetric if, for example, the relations “to stand next to each other on a shelf” on a set of books or “to be relatives” on a set of people are symmetrical.

Asymmetry . A relation R, defined on a set M, is called asymmetric if in asymmetric relations of two relations and no more than one (one or not one) can be satisfied. An example of an asymmetrical relationship: “to be a father” (if he is a father, then he cannot be a father).

Antisymmetry . A relation R defined on a set M has the property of antisymmetry if This means that if the relations are simultaneously satisfied, all relations of a non-strict order are antisymmetric: “to be no more”, “to be no higher”, etc.

Transitivity. A relation R defined on a set M is transitive if for any of the satisfiability conditions

relations follows Formally, this can be written as follows: A relation that does not have such a property is said to be intransitive. For example, the relation “standing next to each other on a shelf” is intransitive. Indeed, let the volumes of some encyclopedia be in ascending order of volume numbers. Then, if the first volume stands next to the second, and the second next to the third, then, obviously, the first does not stand next to the third.

All general properties of relations can be divided into three groups: reflexivity (each relation is reflexive or anti-reflexive), symmetry (a relation is always either symmetrical, or asymmetrical, or antisymmetrical), transitivity (every relation is transitive or non-transitive). Relations that have a certain set of properties are given special names.

How to develop reflection

The best way to learn a skill is to start practicing it. To develop reflection, you need to start practicing it.

How to do it?

Try to understand what feelings you are experiencing at the current moment. The habit of being attentive to emerging joy, anger, melancholy and connecting them with ongoing events or communications with certain people.
Monitor stories in which you react too harshly, painfully. If certain events hit you particularly hard, you need to understand what the trigger is.
If you notice that in the process of thinking about something you experienced melancholy or painful emotions, then it is better to stop soul-searching and return to the roots of the problem a little later. Highly sensitive people cannot do without the help of a specialist.
Give up total control of reality. Reflection is not a reason to put the material world into pieces. Allow life to flow outside of your participation.
In the evening, you can “scroll” your day in your head, all its pros and cons, and form plans for tomorrow.
To develop reflection, make it a rule to think systematically about any phenomenon or object that interests you.

After gaining reflection skills, you can ask yourself a few questions and give honest answers to them:

Think about whether there is something in the past that would be worth returning to and trying to start over. This could be family, work, hobbies, friends, etc. Sometimes a return to the past means the beginning of a new stage.
Clearly establish for yourself what brings pleasure and makes you happy. This will be the strategic goal to which you should devote your future life.
If you are not happy with the point you are in now, determine the actions you need to take to get out of it. Do not slip into self-flagellation or attribute all problems to external circumstances.
Truthfully answer the question of what you are doing wrong. You should not wring your hands with the question: “Why do I need this?” Take responsibility for failures personally. Where was the mistake, the flaw? The truth can be unpleasant, but without it it’s difficult to fix anything.
If you fail at a question, analyze whether everything possible has been done or whether you can try something else.
Analyze actions from the point of view of achieving the goal. This does not mean that you cannot be spontaneous and that you need to think through every step. However, when time is short, prioritization becomes necessary.

There is an opinion that the purpose of life is life itself, getting pleasure from it and those things that correspond to our internal needs. Reflect wisely, achieve what you want and be happy!

Logical reflexivity

In the theory of knowledge and in logic, essentially the same reflexivity operates; this is logical reflexivity. The transformation of a subject into an object and the transfer of an object into a subject, or representation, in the process of cognition, transcendental to immanent (this problem, as is known, represents a puzzling problem of modern philosophy) is possible only thanks to logical reflection, namely the logical reflexivity of the categories of the logical. As we already know, some categories of ontology are at the same time categories of the logical (categories of being, essence, identity, contradiction-negation, etc.). Their logical reflexivity in a unique form introduces the real into the logical. This ensures the objectivity of the logical, logical (non-objective logical, as we know, is impossible). Such categories of the logical that do not belong to ontology and belong only to the logical sphere (for example, the concept of a category, the concept of a concept, the concept of a judgment) are objects of themselves. This does not mean representing the subjective as objective; no, this is the complete implementation of logical objectivity, since in the reflexivity of these categories complete logical necessity is realized, the need for self-justification through the negation of oneself, i.e. the most objective thing that can be imagined logically.

Reflexivity operates in cognition, since both knowledge and cognition of cognition, as knowledge of knowledge, are true (this question, as we know, was first raised by Socrates; Plato’s “Theaetetus” and other dialogues explore precisely this problem). What is knowledge? The answer to this question cannot but contain reflectivity. What are the logical conditions of knowledge, science? The answer to this question is the main content of epistemology, the foundation of which was laid by Kant. Understanding the nature of knowledge is knowledge of knowledge. What are the forms of knowledge? In what forms does knowledge ultimately exist? The answer to this question and the content of logical forms of knowledge coincide with each other. Epistemology is the science of logical forms of knowledge. But logic, as a science, is also a science of forms of knowledge, scientific knowledge about the logical forms of knowledge. In this sense, epistemology and logic are one and the same; The same logical reflexivity is essential for both epistemology and logic.

The method of cognition, knowledge, cannot but be a logical method. Even when the theory of knowledge is based on psychologism, the ability of cognition is used as a logical method. In modern positivism, the application of the principle of verification has the meaning of the application of a logical principle. The use of sensations and perceptions as a criterion of truth gives them not only logical meaning, but also, so to speak, the character of a kind of metaphysical principle. The principle that denies the principle of metaphysics is the principle of the new metaphysics and acts in its role.

The proposition that knowledge is based on experience itself goes beyond the limits of experience. Closing oneself within the limits of experience means limiting oneself, defining oneself as inexperienced, and relying on the inexperienced. Establishing a boundary also means overcoming it (as Hegel said to Kant).

The logical method of knowledge is not given to logic in advance; The method of logic is at the same time its subject. Deductive logic studies the deductive method implemented in forms of thought, in particular in inferences; Also, the subject of inductive logic is the inductive method, implemented in inductive inferences. Reductive logic makes its subject matter the reductive method, etc. This also applies to dialectical logic. The subject of dialectical logic is the dialectical method, implemented in logical forms of thought, the dialectical method as a method of proof (more on this later). Consequently, the logical method, as a means, is for logic, at the same time, an object. Therefore, it must be said that logic, according to its nature, is reflexive.

Consideration of the dialectical method itself has a dialectical nature; knowledge of this method is dialectical. The reflexivity of logic is also essential for the theory of knowledge. The dialectical method of cognition and the dialectical method of logic are one and the same method. It contains the same laws and forms. Categories, as objective means, are also applied in relation to them: this is one and the same thing, essential both in the theory of knowledge and in logic. The application of the same form to a logical form is logical reflexivity. For logic, the concept of a concept, judgment about a judgment, the dialecticity of the concept of dialectics, etc. are essential. Consideration of a syllogism using the form of a syllogism, the use of dialectical inferences or judgments when considering the dialectical method are at the same time both logical and cognitive reflection. Therefore, logic, theory of knowledge and dialectics are one and the same.

Logic is reflexive in nature also in Aristotle, whose logic is called the logic of being; the logic of being is distinguished from the logic of reflection (for example, Günther)[186]. Such a distinction is incorrect, since logic cannot but be reflexive. Logic studies precisely the logical; logical forms were always considered using these forms, etc. But the inferential form of logical reflection was discovered only at the highest stage of development of logic. This inferential form cannot be given in many-valued logic (as Günther believes) since it is a mathematical science. The inferential form of logical reflection is represented only by infinite inference, as has been sufficiently proven and shown above.

True, logic has always been reflexive, but the doctrine of this reflexivity was first developed by Hegel (based on Fichte) in his dialectical logic. From Hegel's point of view, the categories of essence are reflexive; if in the categories of being there is a transition to another, then in essence - in relation to oneself - there is a certain circulation - a circle, where reflexivity means a kind of relativity: the “transmission” of one category into the second and vice versa - the basis is “visible” in the consequence and vice versa, condition in the conditioned and vice versa, cause in the action and vice versa, etc.

Therefore, the logical reflexivity we recognize is essentially different from the reflexivity that Hegel speaks of (we mean only the logical side of the reflexivity considered by Hegel, neglecting the mystical side). The logical reflexivity we recognize is rather similar to what Hegel calls the “subjectivity” of the concept. The concept for Hegel is self-foundation and self-development; the “subjectivity” of a concept consists in the fact that the concept represents self-justification; the concept is a generality, but it is also a particularity; the unity of both is singularity. The concept, as a single concept, contains in itself generality and specificity. These three points exhaust the nature of the concept. The concept is unity returned to itself.

The logical reflexivity we recognize, however, is similar to the “subjectivity” of Hegel’s concept, but, in fact, is essentially different from it, because; 1) As was clarified above, Hegel’s “particular” hides opposition-contradiction, while in the reflexivity of infinite inference the unity of opposites is fully realized. 2) For Hegel, the concept, as a community, exists. the mystical ability of the absolute to address itself, while the reflexivity of the category of the logical, realized in endless inference, does not contain anything illogical. 3) Hegel was unable to give a form of dialectical inference; he limited himself to formal logical conclusions, although the “rational grain” of his dialectics required going beyond the conclusions of old logic. 4) That is why for Hegel the highest inference remained the dividing inference, which is the mode of the third figure (E-B-O), while for us the highest form of inference is the infinite inference.

For us, reflexivity is internal self-affirmation (and not the action of the mystical ability of self-knowledge of the absolute, as represented by Hegel). Reflexivity should not be reduced to identity or equality, to a relation to oneself (xRx) without internal difference and negation. Without internal difference and negation, logical reflexivity does not occur. And with identity, as we know, there is difference; “A is A” means: “if there is A, then there is A,” here: “if there is A” (unstated A) is different from “there is A” (from asserted A). (As for the reflexive relation of mathematical logic, it represents equality, more precisely: a relation that is reflexive, symmetrical, and transitive is called equality or equivalence. [187] But this is a purely mathematical concept to which logical reflexivity cannot be reduced).

Consequently, we can say that in the aspect of logical reflection, dialectics, logic and theory of knowledge are one and the same. This is so precisely from a logical (and not from a psychological or other) point of view.

Logic as organon

Logic, as a reflexive science of logical reflection, cannot but be an “organon”, not only in the ancient sense of the word, but also from the point of view of “higher logic”, in the dialectical-logical understanding. Logical means and forms are used not only in every science, in knowledge in general, but, as was said, they are also used in relation to them. That is why they have the meaning of logical reflection. The categories of logical represent objective logical means - “tools” of any knowledge in general. Therefore, logic is an “introduction” to all sciences, to knowledge in general, including logic itself. Logic, as an “introduction,” is general, that is, it contains itself.

Here, for our purposes, it is enough to consider only two questions: 1) the absoluteness of the science of logic in relation to other sciences and 2) the identity of the rules of logical and cognition.

As has been said, only one logic is possible; accepting more than one logic constitutes a logical fallacy. Therefore, we can say that logic has an absolute character, it is such in relation to other sciences. This - being in relation to another - does not abolish its absolute character; no, it contains a relationship to another, since logic itself is one of the sciences and its absoluteness lies precisely in the fact that it is a science and at the same time a theory of science.

The logical forms of thought are the same for all sciences; they are forms of knowledge in general (including the science of logic). The logical means and forms of all knowledge or knowledge are the same. Such means and forms represent the subject of logic and their consideration is carried out by these same means and forms.

Logic is applied in every science; science is impossible without the use of logic, since knowledge exists in the form of logical forms - concepts, judgments, conclusions, evidence. Logic also applies science, since the subject of logic is the forms of scientific knowledge and knowledge in general. The achievements of science, the results of the development of science are reflected in the concepts and categories that logic studies. But the application of logic by sciences differs from the application of logic by other sciences, since special sciences use logic as their own logical basis, but are not themselves the logical basis of logic. Material, examples, including exemplary ones, are provided to logic by other sciences; for example, as noted above, mathematics (Cantor) was able to positively define infinity. Therefore, logic is forced and it has become possible for it to establish a general logical positive concept of infinity. When logic applies other sciences, the same logic and its means are used. The logic is the same. The application and use of the other is and must be carried out on the basis of logic itself, otherwise we must admit the need for another logic, the existence of two logics.

Special sciences differ from each other in their subjects. In general, each science is determined by its subject; Science is certain knowledge because it is knowledge of the subject. Science, of course, does not exist without a subject, but, on the other hand, it cannot exist if logic is impossible. Every science is a science due to logic. Science is a system, without a system it is impossible; but the system is proof, a system of proof. The system of science, as a system of proof, is logic implemented in the material of science. For example, Euclid's system of geometry is a system compiled on the basis of some provisions of Aristotle's logic, a system where the material is geometric, and the systematicity itself represents a logical connection. Therefore, we can say that “all science is applied logic”[188]. For example, in “Capital” by K. Marx, as a private science, logic, dialectics and the theory of knowledge are used, which represent one science[189]. The dialectic of “Capital” is a special case of dialectics[190]. This applies to other sciences as well. Logic is not logically based on anything. She proves herself by her own means. In this sense, logic has an absolute character.

In view of the above, logic cannot rely on the method of private science, for example, on mathematical methods, as some followers of mathematical logic require. The application of the mathematical method to logic would transform the latter into mathematics. If the mathematical method contains all logical means, then mathematics will turn into logic - into a universal science, i.e. only the name will change, but the nature of the logic will remain the same. If the mathematical scheme replaces logic, then logic as a science will be eliminated. This is the case at least (partially) when logic is considered a "general scheme" model. Logic is a science, a theory. It is impossible to imagine logic without theory. Each logical scheme has some meaning and it is the meaning that is included in the subject of logic. Theory is understanding, thought, and when we are dealing with logic, then we must say that logic is a theory about the logical, and the logical is a connection of thoughts, presented in the form of a thought (and not a diagram).

Logic, as a theory about itself, cannot but be, at the same time, a theory of knowledge. If logic is dialectical, then dialectics, logic and theory of knowledge cannot but coincide with each other.

The method and rule of knowledge must be the method and rule of obtaining new knowledge. If the logical is synthetically logical (and this, as has been shown, is so), then the logical rule is also the rule for obtaining something new. Due to the above-mentioned absoluteness of logic, its method and fundamental rule must be a universal method and rule. This rule of obtaining something new and the rule of knowledge must be one and the same. This should be the rule of logic as an instrument - an “organon”. A logical objective means - an instrument - is used in general in science and in logic. This reflexivity, as we know, identifies the cognitive and the logical, and since the synthetic-logical has a dialectical nature, this identity also contains dialecticity, it is dialectical.

A transition in the logical, as a transition to something new, is a conclusion, the implementation of logical necessity. But this transition, like receiving something new, is at the same time a “discovery”. Therefore, in logic the path of proof and the path of discovery are identified with each other; the rule of evidence and the rule of discovery must represent the same rule. The implementation of the deductive method must represent the acquisition of something new, since deduction, as a transition from the general to the particular, is a transition to the opposite. Induction is also a transition to the opposite, since it is a transition from the particular to the general. Therefore, the rule of evidence and the rule of discovery must be a dialectical rule, a rule of logical development, in the aspect of which dialectics, logic and the theory of knowledge will be one and the same (the rule indicated here will be specifically discussed below).